Sim, é verdade. E a afirmação do título não contém qualquer ironia.
Todo mundo aprende na escola que a menor distância entre dois pontos é uma reta. Mas pouca gente se recorda – e alguns professores se esquecem de avisar – que isso é válido apenas em um espaço plano. Em um espaço tridimensional, a coisa muda de figura.
Imaginemos, por exemplo, um triângulo equilátero, aquele em que todos os lados são iguais e todos os ângulos internos somam 180 graus.
Marcando dois pontos dentro do triângulo, a menor distância entre eles sempre será uma reta. Além disso, não importa o tamanho dos lados: sempre, em qualquer circunstância, a soma dos ângulos internos do triângulo será 180 graus.
Pois bem. Vamos mudar, agora, o paradigma. Imaginemos um espaço tridimensional, tipo aquele em que nós vivemos todos os dias. Além das duas dimensões existentes no plano bidimensional (altura e comprimento), há uma outra: a profundidade.
Nesse tipo de plano, a menor distância entre dois pontos é uma curva, mais especificamente um arco de círculo máximo. E – o que parece mais bizarro – a soma dos ângulos internos de um triângulo não é 180, mas 270 graus.
Duvida? Veja a figura:
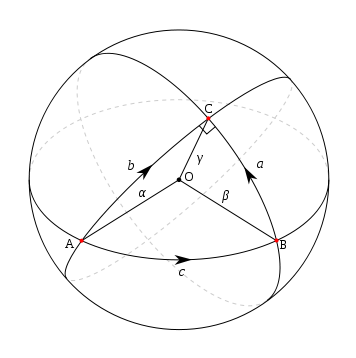
Repare que o triângulo formado entre os pontos A-B-C possui três ângulos retos (90 graus). Portanto, 270 graus.
Ainda tá duvidando?
Vamos trocar a imagem da esfera por algo mais familiar: a Terra.

Note que, nesse exemplo, a base é formada pela linha do Equador. Com qualquer meridiano, o ângulo formado com o Equador será de 90 graus. Seguindo-se um meridiano qualquer até o pólo norte e, de lá, seguindo-se outro meridiano até o Equador, teremos mais dois ângulos retos.
“Ok. Mas qual é a importância prática disso?”
Seguinte: quando você voa num avião, por exemplo, a trajetória que ele fará para ir de um destino a outro não seguirá uma “linha reta”, como muita gente imagina. Ele seguirá a “curva” da Terra, fazendo pequenos ajustes no sentido da viagem de modo a percorrer o menor trecho possível. Se ele fosse simplesmente “reto”, acabaria por percorrer uma trajetória maior do que a se seguisse a curvatura terrena.
Uma imagem pode, por exemplo, demonstrar como uma viagem entre Nova Iorque e Lisboa é feita, seguindo-se a menor distância entre dois pontos em um espaço tridimensional.
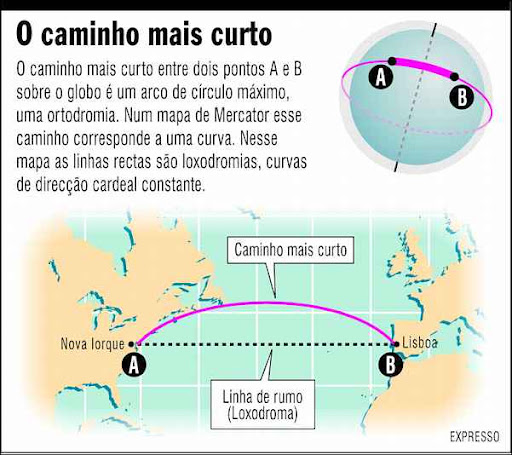
Além do exemplo do avião, essa demonstração serve para você refletir. Questionar certezas e mudar paradigmas é o primeiro passo para descobrir todo um novo universo. Basta ter curiosidade e disposição para isso.

É importante que se diga; curva só no mapa, na vida real é uma reta mesmo.
Outra coisa muito importante; estes ângulos de 90 graus só serão encontrados obedecendo a junção dos círculos (máximos), não se pode escolher 3 pontos a esmo como num mapa e tais ângulos devem partir do centro (de um objeto 3D).
É verdade, Francisco. Provavelmente deixei passar em branco isso no corpo do texto, mas agora quem o ler já estará avisado. Um abraço.
A trajetória pode ser vista como uma curva sim. E na vida real ou não a melhor nomenclatura para ela é geodésica.
Fiquei na mesma. Se a curva pode ser caminho mais curto entre dois pontos, mas só no mapa, qual a aplicação real desse conhecimento?
Mais ou menos, Comandante. Na verdade, esse “só no mapa” não é bem o que acontece. Embora numa trajetória digamos, “real”, o objeto se mova “em linha reta”, observando-se esse mesmo objeto movimentando-se no espaço tridimensional, na verdade, ele se move “em curva”. Isso faz toda a diferença na hora de se calcular rotas e distâncias nos espaços tridimensionais. Um abraço.
A mesma da teoria da relatividade fe Einstein.
Identifico aqui, talvez um equívoco conceitual, pois estritamente reta é um objeto geométrico infinito a uma dimensão.
Confesso que não entendi o comentário, Arcanjo. Você poderia explicar melhor onde estaria o equívoco conceitual?
A menor distância entre dois pontos é um segmento de reta. Pois um segmento possui uma origem e um fim. Já uma reta pode possuir origem, porém não possui um fim. O erro conceitual é que você usou o termo “reta” como usamos coloquialmente e não no seu conceito original. Abraços.
@Gustavo Lopes –
Na verdade, retas não podem possuir origem. Semi-retas sim.
Obrigado, Henrique. Fica aqui o registro. Um abraço.
Adorei o assunto e os comentários controversos,pois é isso que faz o conhecimento de uma pessoa, estado, nação evoluir.Agora não vou cair nas afirmações dos meus amigo que afirmam: “a menor distância entre dois pontos é uma reta “.
Parabéns pelo trabalho, rapazes.
Falta você estudar geometria, porque ? Somente Euclides, disse que a menor medida entre 2 pontos é uma reta. : Puro equívoco: a menor medida entre 2 pontos é realmente uma curva, estude geometria espacial, trigonometria esférica, veja que todos vocês estão equivocados. ok
Vaai Estuda Geometria Esfesrica e espacial Vaai aprende isso e nao cretica meeu paai nao que sabe mais que voces
A menor medida entre dois pontos está entre as paralelas sobrepostas.
Eu sou fiel ao trabalho do Euclides, pois, se andássemos em linha reta, os quatros lados de um retângulo, partindo de A a D, com certeza andaríamos mais. Então, a menor distância entre dois pontos, são as diagonais desse retângulo ABCD.
A afirmação de que a menor distância entre dois pontos é um segmento de reta é um postulado da geometria plana. Não é possível provar exatamente porque é postulado. Se alguém conseguir uma menor distância entre dois pontos que não seja o que hoje chamamos de segmento de reta, então esta nova linha, seja ou não seja reta ou segmento, é que será segmento de reta. Ah! E na Terra a menor distância entre dois pontos é e continua sendo um segmento de reta, só que não é possível nos deslocarmos pela menor distância.
Até que enfim alguem que pensa de forma simples e objetiva.
Só fico em dúvida se aí já não estaríamos sendo preciosistas demais, meus caros. Lembrem-se de que este blog não é de físicos ou dedicado inteiramente à Física, mas, sim, ao público leigo em geral. Logo, não vejo maiores problemas em usar um pelo outro, já que o que se pretende aqui é apenas tentar explicar o conceito para quem não é versado no assunto. Um abraço.
Isso mesmo… Eu já vi o super-homem fazer isso na TV e o Mario Bros saindo do Japão e chegando lá no maracanã na abertura das olimpíadas 2016… Você têm razão.
Ótimo texto, gostaria porem de apontar um equivoco na parte do texto que diz: ”E – o que parece mais bizarro – a soma dos ângulos internos de um triângulo não é 180, mas 270 graus.”
Isso na verdade só ocorre em casos específicos, é verdade porem que tal soma é sempre maior que 180 e menor que 540, não sendo sempre constante, fato igualmente notável.
Tem razão, Pedro Henrique. Obrigado pela observação. Quem ler os comentários agora vai ficar sabendo disso. Um abraço.
Partindo do pressuposto de uma viagem sobre uma esfera (terra, que no caso não é uma esfera perfeita, mas consideremos) qualquer viagem que seja feita, a trajetória será curva, ou seja, mesmo que se viaje sobre uma “linha” de circulo máximo e equipotencial. A única forma neste caso de viajar em uma linha reta seria fazer um buraco na terra para chegar até o outro local ( isso para grandes distancias claro, para ir até o seu vizinho isso não seria viável, pois para pequenas distancias podemos considerar a curvatura do planeta desprezível) Imagine uma viagem de São Paulo até Hong Kong, por mais que voce quisesse essa viagem nunca seria uma reta, será aproximadamente, se for o caminho mais curto, a metade de um circulo. Agora imagine que posse possível construir um túnel que ligasse as duas cidades atravessando o planeta, teríamos então uma reta e o caminho seria muito mais curto do que percorrer uma curva sobre a terra, ja que percorrer uma reta sobre uma esfera da forma que esta sendo tratado aqui é impossível. As afirmações de euclides estão corretas para um espaço euclidiano, uma esfera não é um espaço euclidiano. Outro problema é imaginar a rota do avião, esta é corrigida a cada instante, pois se seguir apenas a referencia magnética da terra a trajetória será descrita de forma equivocada, mas essa explicação é um pouco mais longa.
Ainda bem que li tudo e não tive que escrever isso. SEMPRE um segmento de reta será a menor distância entre dois pontos, não significa que a menor distância é a mais rápida ou a que demanda menos esforço por parte de quem está transitando. Um exemplo é que se você tem um muro de 15 metros de comprimento, 5 metros de altura e 2 metros de espessura, para atravessar o caminho mais perto é você quebrar o muro e fazer uma passagem. No entanto isso demanda mais esforço e energia do que pulá-lo ou cavar um buraco por baixo do muro. Também não pulamos 5 metros de altura, então dar a volta lateralmente e pegar o caminho mais longo, é o que demanda menos esforço e gasta menos energia, mesmo que seja o mais longo. Aí entra a parte do tráfego. As vezes quando se percorre um espaço qualquer seja no trânsito de automóveis, pedestres ou aeronaves o mais prudente é tomar a rota mais longa pois não adianta você tomar uma rota curta de baixa mobilidade. Pra ficar bem exemplificado imagine que você vai do seu trabalho pra sua casa pelo caminho mais curto e percorrer 5 km de engarrafamento em 1 hora. E se desse a volta por outras rotas menos usadas você percorreria 20 km porém chegaria em 30 minutos.
Só uma coisa, Gustavo. Distância não tem nada a ver com o tempo (deixando-se de lado o conceito de continuum proposto pela Teoria da Relatividade). Quando se fala na menor distância entre dois pontos, obviamente ninguém está se referindo ao menor tempo a ser coberto entre o deslocamento entre dois pontos. É claro que ir de uma cidade a outra por uma autoestrada com 4 pistas de cada lado e asfalto perfeito é mais rápido do que ir por uma estrada de piçarra cheia de buracos, ainda que a primeira seja um pouco maior em quilometragem. A questão, como está escrito no post, é trazer a atenção do público para conceitos nem sempre bem compreendidos pela maioria. Um abraço.
Muito bom Pacuera, eu estava prestes a escrever o mesmo até ver seu comentário rsrsrs
Entre leigos, essa é uma discussão interminável. Entre conhecedores do assunto, simplesmente não existe dúvida.
entendi perfeitamente a linha de reciocinio perfeitamente, isso amigo parabéns mesmo eu que não tenho muita formação pude entender, parabéns isso vai mudar muito a minha forma de análise.
Obrigado, Robson. Um abraço.
NA MINHA OPINIÃO, SOU LEIGO, MAS QUERO APRENDER, A MENOR DISTANCIA ENTRE DOIS PONTOS É UM PONTO!
Poderiam ser mais claro kkk, eu entendi que nem sempre a distancia entre 2 pontos é so ir em frente e sim fazer algumas adaptações, sei la, contornar algumas situações…
Eu fiquei em dúvida, essas afirmações vem do pressuposto de que atravessar a terra, como um túnel, é impossível? Porque não consigo imaginar como o arco formado por 2 pontos ser menor que a reta que os ligam
ok esse conceito está errado ! a mentor distancia entre um ponto e outro sempre será uma reta, desconsiderando é claro que o espaço se curve como prevê a teoria da relatividade. e a prova matemática para isso é simples !!! vejamos :
consideramos uma esfera de raio r
perceba que r é igual a distancia do ponto “AO” ou “OC” (na segunda figura) muito bem
perceba que se eu for uma formiga e caminhar do ponto “A” ao “C”, certamente eu percorreria 1/4 do comprimento da circunferência, logo eu percorria 2*pi*r/4 = pi*r/2
no entanto se eu percorresse uma linha reta do ponto “A” ao ponto “C” eu estaria percorrendo a hipotenusa do triangulo onde seus catetos são “a” e “y” e por pitagoras essa distancia que eu chamarei de “h” seria :
h^2 = r^2 + r^2
logo h = (2*r^2)^(1/2)
logo h = r*(2^1/2)
sendo assim temos que para qualquer raio de circunferência a distancia reta entre 2 pontos será sempre menor pois
(pi/2 = 1,55) > (2^(1/2) = 1.4142)
sendo assim para um raio da terra que é aproximadamente 6371 km
indo de avião do brasil para o polo norte. andaríamos com certeza 800 km a mais que se pudêssemos ir em linha reta .
🙂
Concordo!
Gostei da idéia de questionar, de propor novas teses… Mas a menor distância entre dois pontos será sempre uma reta, a menor distância entre duas retas será sempre um plano, a menor distância entre dois planos será sempre um volume e a distância entre dois volumes é assunto para a próxima teleaula… Grande abraço e fique sempre com Deus
Ao minimizarmos uma função para se obter a menor distância entre dois pontos encontraremos uma reta, mas ao minimizarmos para se obter o menor tempo para se ir de um ponto a outro encontraremos uma curva. É o problema da Braquistócrona, muito conhecida nos meios acadêmicos de exatas. https://pt.wikipedia.org/wiki/Braquist%C3%B3crona
Excelente explicação! Inclusive os comentários trazem dimensionamentos que ampliam o conhecimento da proposta inicial.
A menor distância entre dois pontos é uma reta (plano cartesiano).
Mesmo sobre a superfície terrestre a afirmação é válida, o que acontece é que é praticamente impossível percorrer grandes distancia em linha reta sobre o Globo.
A menor distância entre dois pontos opostos e na superfície da terra é uma reta – o diâmetro. Só não é possível percorre-lo. Mas esta linha existe..
A menor distância entre 2 pontos é quando não há distância, ou seja 0. Pegue uma folha e pinte esse ponto de azul, depois pinte de amarelo por cima desse ponto azul, bom, são ainda serão dois pontos diferentes, ocupando um mesmo espaço, estando exatamente juntos.
Eu não concordo. A menor distância entre dois pontos do globo terrestre continua sendo uma linha reta, no caso essa linha hipotética passaria por dentro do globo.
eu gostaria que vc explicasse com conceitos da física pq isso ocorre?
Parabéns ao autor do blog e a todos que participaram da discussão, pela exposição das ideias, pela condução ética da discussão e pelo respeito mútuo entre os participantes, ante as divergências das ideias.
Obrigado, Antonio. É justamente para isso que esse espaço foi criado. Um abraço.
A menor distância entre 2 pontos não coincidentes não é um segmento de recta mas sim uma sinusoide com amplitude insignificante que faz parecer um segmento de recta. Essa mesma sinusoide poderá ter andamento curvo na sua trajectória dependendo dos obstáculos que vá encontrar(exemplo: avião). De notar que a amplitude da sinusoide pode variar consoante as condições(exemplo: percorrer “100m” em trajectória sinusoidal com amplitude insignificante quando se está sóbrio é bem diferente de quando se está trôpego em que a amplitude foi accionada). Esqueçam o que se aprendeu na escola e verifiquem que no Universo as leis da Física se regem por ondas magnéticas e que são sinusoides. A luz também não se propaga em linha recta como nos ensinaram, As distâncias que divulgamos são do nosso imaginário, não são exactas. O tempo é intemporal e o Espaço espacial…………… parabéns pelo blog
Pegue um papel sobre uma mesa e vc saberá perfeitamente que a menor distância entre qualquer ponto será uma reta! Ainda bem que isso já foi provado(por ser óbvio) que não se aplica a grandes distâncias porque nosso espaço é tridimensional! E a terra não é plana! E que nosso mapa não é representado de forma plana, mas UTM(Universal transverso de mercado) melhor representado quando se quer demonstrar áreas em um globo. Agora, se vc quer simplificar, use um mapa mundi convencional, mas deixe claro que ele não encaixa de forma nenhuma na terra e é impraticável, pois obedece o senso comum como ocorre em Euclides. O problema, senhores, está no senso comum que obedece uma lógica clara e fácil de compreender por simples interpretação do cérebro, mas o espaço tridimensional no qual estamos inseridos é meio complexo tanto quanto a designação de uma reta ou segmento, isso pq a própria proposta pode ser equivocada, pois não podemos esquecer de mencionar a mesa, ou seja, o espaço bidimensional que, digamos, é bem restrito numa bola! Chega a ser cômico tal dúvida.
Dois eixos nessa “curva seriam “retos”, no caso o x e o y e o z (altura) seria o que faz uma variação de altura?
A menor distância é sempre uma reta. Se o avião pudesse perfurar a terra para percorrer a menor distância, ele faria. O conceito é teórico e não considera limites de um geodo
É, eu estou ainda aprendendo, eu sabia q era uma reta, gostei da explicação, bem coerente.
Se vivemos em um globo, não tem como ir de um ponto ao outro em linha reta, em grandes distâncias.